Catatan Harian Jurnalistik, Elektronika Dan Umum: kontruksi rumus GGL (Gaya Gerak Listrik)

Michael Faraday bapak penemu listrik, menemukan bahwa GGL (Gaya Gerak Listrik) hasil induksi magnet bergantung pada laju perubahan fluks magnetik yang melalui suatu kumparan.
Telah kita ketahui seperti halnya hari ini, bahwa sebuah baterai akan mengalirkan arus listrik melalui suatu rangkaian tertutup. Apabila arus listrik mengalir didalam suatu rangkaian maka disekitar arus tersebut akan timbul fluks magnetik (Lihat: Hukum Biot-Savart). Kemudian muncul suatu pertanyaan, bagaimanakah hubungan antara GGL hasil induksi dengan fluks magnetik??
Pertanyaan itulah yang coba dijawab oleh Michael Faraday. Melalui penelitiannya ia menyimpulkan bahwa:

GGL Induksi yang timbul di antara ujung-ujung suatu loop penghantar berbanding lurus dengan laju perubahan fluks magnetik yang dilingkupi oleh loop penghantar tersebut

Kesimpulan ini didapatkan setelah ia melakukan serangkaian percobaan dengan cara menggerak-gerakkan sebatang magnet kedalam sebuah kumparan kawat penghantar. Dari sini ia mengetahui bahwa perubahan kerapatan fluks magnetik mengakibatkan perubahan potensial listrik pada ujung-ujung kumparan kawat penghantar.
Secara matematis, hukum faraday dirumuskan sebagai berikut:

Konstruksi	Rumus	Besaran (SI, kecuali disebutkan khusus)
Lilitan silinder	$L=\frac{\mu_0KN^2\pi r^2}{l}$	L = induktansi μ₀ = permeabilitas vakum K = koefisien Nagaoka N = jumlah lilitan r = jari-jari lilitan l = panjang lilitan
Kawat lurus	$L =200 \, l \left(\ln\frac{4l}{d}-1\right)10^{-9}$	L = induktansi l = panjang kawat d = diameter kawat
Lilitan silinder pendek berinti udara	$L=\frac{r^2N^2}{9r+10l}$	L = induktansi (µH) r = jari-jari lilitan (in) l = panjang lilitan (in) N = jumlah lilitan
Lilitan berlapis-lapis berinti udara	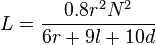$L = \frac{0.8r^2N^2}{6r+9l+10d}$	L = induktansi (µH) r = rerata jari-jari lilitan (in) l = panjang lilitan (in) N = jumlah lilitan d = tebal lilitan (in)
Lilitan spiral datar berinti udara	$L=\frac{r^2N^2}{(2r+2.8d) \times 10^5}$	L = induktansi r = rerata jari-jari spiral N = jumlah lilitan d = tebal lilitan
Inti toroid	$L=\mu_0\mu_r\frac{N^2r^2}{D}$	L = induktansi μ₀ = permeabilitas vakum μ_r = permeabilitas relatif bahan inti N = jumlah lilitan r = jari-jari gulungan D = diameter keseluruhan

[sunting] Dalam sirkuit elektrik

Sebuah induktor menolak perubahan arus. Sebuah induktor ideal tidak menunjukkan resistansi kepada arus rata, tetapi hanya induktor superkonduktor yang benar-benar memiliki resistansi nol. Pada umumnya, hubungan antara perubahan tegangan, induktansi, dan perubahan arus pada induktor ditentukan oleh rumus diferensial:

$v(t) = L \frac{di(t)}{dt}$

Jika ada arus bolak-balik sinusoida melalui sebuah induktor, tegangan sinusoida diinduksikan. Amplitudo tegangan sebanding dengan amplitudo arus dan frekuensi arus.

$i(t) = I_P \sin(2 \pi f t)\,$

$\frac{di(t)}{dt} = 2 \pi f I_P \cos(2 \pi f t)$

$v(t) = 2 \pi f L I_P \cos(2 \pi f t)\,$

Pada situasi ini, fasa dari gelombang arus tertinggal 90 dari fasa gelombang tegangan.
Jika sebuah induktor disambungkan ke sumber arus searah, dengan harga "I" melalui sebuah resistansi "R" dan sumber arus berimpedansi nol, persamaan diferensial diatas menunjukkan bahwa arus yang melalui induktor akan dibuang secara eksponensial:

$\ i(t) = I (e^{\frac{-tR}{L}})$

[sunting] Analisis sirkuit Laplace (s-domain)

Ketika menggunakan analisis sirkuit transformasi Laplace, impedansi pemindahan dari induktor ideal tanpa arus sebelumnya ditunjukkan dalam domain s oleh:

$Z(s) = Ls\,$

dimana

L adalah induktansi

s adalah frekuensi kompleks

Jika induktor telah memiliki arus awal, ini dapat ditunjukkan dengan:

menambahkan sumber tegangan berderet dengan induktor dengan harga:

$L I_0 \,$

(Pegiatikan bahwa sumber tegangan harus berlawanan kutub dengan arus awal)

atau dengan menambahkan sumber arus berjajar dengan induktor, dengan harga:

$\frac{I_0}{s}$

dimana

L adalah induktansi

$I 0$ adalah arus awal

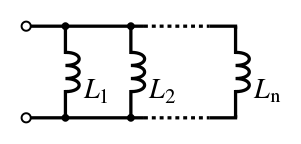
Jejaring induktor

Induktor dalam konfigurasi kakap memiliki beda potensial yang sama. Untuk menemukan induktansi ekivalen total (L_eq):

$\frac{1}{L_\mathrm{eq}} = \frac{1}{L_1} + \frac{1}{L_2} + \cdots + \frac{1}{L_n}$

Arus dalam induktor deret adalah sama, tetapi tegangan yang membentangi setiap induktor bisa berbeda. Penjumlahan dari beda potensial dari beberapa induktor seri sama dengan tegangan total. Untuk menentukan todu total digunakan rumus:

$L_\mathrm{eq} = L_1 + L_2 + \cdots + L_n \,\!$

Hubungan tersebut hanya benar jika tidak ada kopling magnetis antar kumparan.

Energi yang tersimpan

Energi yang tersimpan di induktor ekivalen dengan usaha yang dibutuhkan untuk mengalirkan arus melalui induktor, dan juga medan magnet:

$E_\mathrm{stored} = {1 \over 2} L I^2$

Dimana L adalah induktansi dan I adalah arus yang melalui induktor.
ε : GGL Induksi antara ujung-ujung penghantar (Volt)
N: Banyaknya lilitan kumparan
ΔΦ: Perubahan fluks magnetik (Wb)
Δt: Selang waktu perubahan fluks magnetik (s)

Hukum GGL Induksi Faraday:
Bila suatu magnet permanen digerakkan masuk dan keluar suatu kumparan penghantar maka pada kumparan tersebut akan timbul tegangan listrik (GGL).

Catatan Harian Jurnalistik, Elektronika Dan Umum

Rabu, 23 Maret 2011

kontruksi rumus GGL (Gaya Gerak Listrik)

[sunting] Dalam sirkuit elektrik

[sunting] Analisis sirkuit Laplace (s-domain)

Jejaring induktor

Energi yang tersimpan

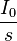
Tidak ada komentar:

Posting Komentar